경사하강법 ( Gradient Descent )
손실함수가 최소가 되는 파라미터(모델의 가중치)의 값(기울기가 0인 곳)을 찾기위한 방법
- 어느 한 점 $ \theta_j^{(n)} $에서의 순간기울기를 구해본다.
- $ \theta_j^{(n)} $에서의 순간기울기의 반대 방향($ -\frac{\partial}{\partial \theta_j} J(\theta^{(n)}) $)으로 조금 이동($\gamma$)시킨다.
- 위의 과정을 순간기울기가 0으로 수렴될 때까지 반복한다.
위의 과정을 공식으로 나타낸다면 아래와 같다.
$$ \theta_j^{(n+1)} = \theta_j^{(n)} - \gamma \frac{\partial}{\partial \theta_j} J(\theta^{(n)}) $$
여기서 $ \gamma $를 학습률(Learning rate)이라 부른다.
적당한 학습률로 경사하강법을 충분히 많이 반복하면서 파라미터을 갱신하면 손실함수가 최소값으로 수렴한다.
파이썬 코딩을 통해서 경사하강법에 자세히 알아보자.
손실함수 $J$는 기울기와 절편에 대해서 2차 함수이므로 가장 단순한 $x^2$을 함수로 갖는다고 가정하자.
import numpy as np
import matplotlib.pyplot as plt
x_ = np.arange(-4.5,4.5,step=0.1)
y_ = x_**2
plt.figure(figsize = (8,6))
plt.plot(x_,y_)
plt.xlabel('theta')
plt.ylabel('Loss function J')
plt.show()
만약 첫 파라미터(모델의 가중치 ; 모델의 기울기 또는 절편)을 4라고 가정한다면
plt.figure(figsize = (8,6))
plt.plot(x_,y_)
plt.scatter(4, 4**2, s=200, c='r')
plt.show()다음과 같은 손실함수 값을 가지게 된다.

여기서 경사하강법을 이용하여 0.01의 학습률로 5번 반복한다면
x = 4
y = x**2
lr = 0.01
iter_ = 5
plt.figure(figsize = (8,6))
plt.plot(x_,y_)
plt.xlabel('theta')
plt.ylabel('Loss function J')
plt.scatter(x,y, c='r', s=200)
for _ in range(iter_):
dy_dx = 2*x
x = x - lr*dy_dx
y = x**2
plt.scatter(x,y, c='g', s=200)
plt.show()
이렇게 점점 그래프의 선을 따라 내려가게 되기때문에 경사하강법이라 부른다.
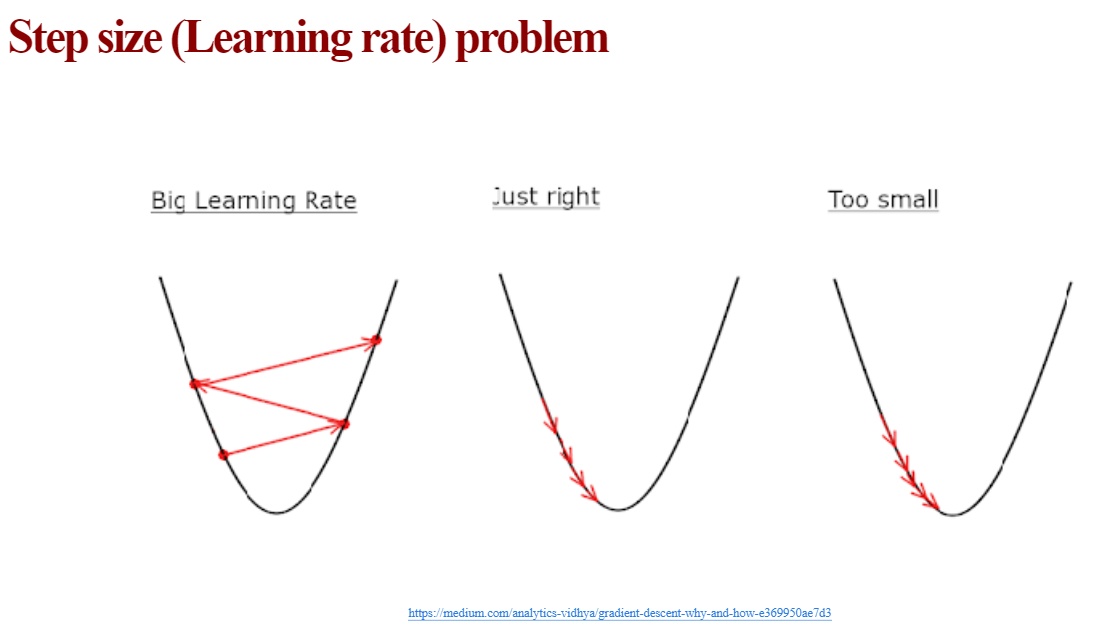
위의 그래프는 너무 작은 학습률과 적은 반복횟수로 손실함수가 최소가 되는 곳까지 내려가지 못했다.
이번엔 학습률을 1.2로 크게 준다면
x = 4
y = x**2
lr = 1.2
iter_ = 5
# ~ 생략 ~
다음과 같이 수렴하지않고 오히려 발산하게 된다.
이번엔 학습률을 0.1로 주면
x = 4
y = x**2
lr = 0.1
iter_ = 5
# ~ 생략 ~
적당한 속도로 내려가고 있는 것을 볼 수 있다.
이제 학습률을 0.1로 고정하고 반복횟수를 50번으로 늘린다면
x = 4
y = x**2
lr = 0.1
iter_ = 50
# ~ 생략 ~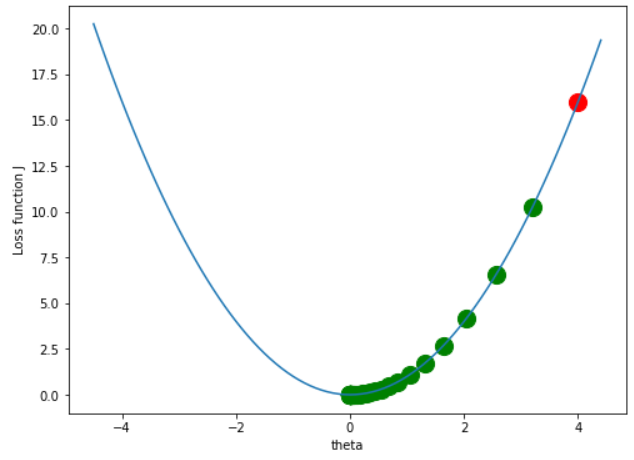
손실함수가 최소가 되는 곳으로 수렴하는 것을 볼 수 있다.
그렇다면 학습률을 0.01로 주고 반복횟수를 500회 한다면
x = 4
y = x**2
lr = 0.01
iter_ = 500
# ~ 생략 ~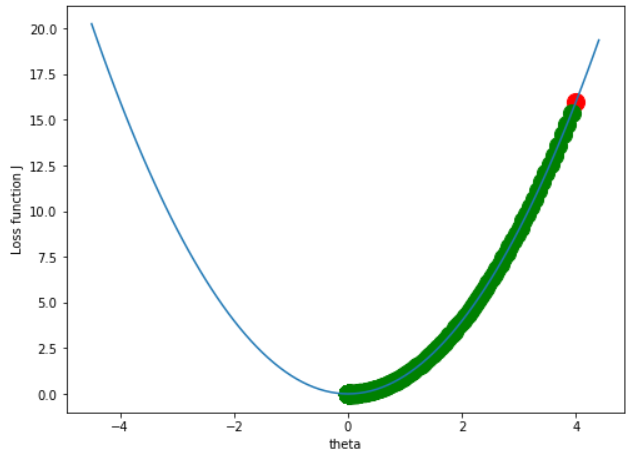
프로그램이 돌아가는데 시간이 좀 걸리긴했지만 손실함수가 최소가 되는 곳으로 수렴하는 것을 볼 수 있다.
따라서 작은 학습률로 최대한 많이 반복한다면 손실함수가 최소가 되는 곳으로 수렴하는 곳을 비교적 정확히 찾을 수 있게 된다.
하지만 너무 작은 학습률로 많이 반복시킨다면 그만큼 시간이 많이 걸린다.(비용증가)
복잡한 모델에서의 손실함수
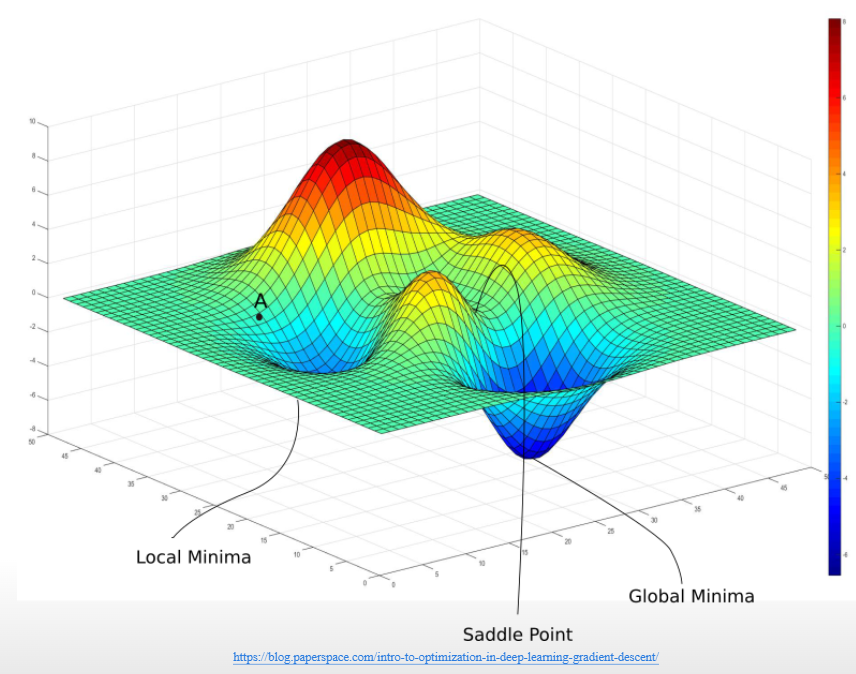
이런 모델에서 경사하강법을 사용한다면 보통 3종류의 최저점을 찾게 된다.
Global Minima
우리가 찾는 곳이다.
Saddle Point
어느 한 단면에서 봤을 때 아래로 볼록한 그래프가 되어 Saddle Point로 수렴하는데, 이럴때 다른 단면(파라미터)로 움직인다면 빠져나올 수 있다.
Local Minima
보통 골이 얕기 때문에 학습률을 한 번 크게 주어 발산하게 만든다면 빠져나올 수 있다. (Cosine Annealing learningrate)
보통 임의의 점 100개찍고 각 점에서 경사하강법을 적용하여 Global Minima를 찾는 방법으로 문제를 해결할 수 있다.
'AI > 기초' 카테고리의 다른 글
| 시그모이드(로지스틱) 함수와 소프트맥스 함수 (0) | 2022.04.14 |
|---|---|
| 뉴럴 네트워크(Neural Network)의 구조 (0) | 2022.04.14 |
| 선형회귀모델로 보는 가중치(기울기,절편) 찾기 ; 최소제곱법(OLS)과 손실함수(Loss function) (0) | 2022.04.14 |
| 인공지능(AI)을 이해하기 위한 수학 기초: 미분 (0) | 2022.04.12 |
| 인공지능(AI)을 이해하기 위한 수학 기초 : 행렬, 로그, 지수, 시그마 (0) | 2022.04.12 |



댓글