실제 $i$번째 데이터
$x_i$, $y_i$
일반적인 선형 회귀 모델
$$ y = \omega_0 + \omega_1 x_1 + \omega_2 x_2 + ... $$
특징이 1개이고 1차항인 선형 회귀 모델
$$ y = \omega_0 + \omega_1 x_1 $$
예측하는 선형 회귀 모델
$ \hat{y} = y$의 추정치, 예측값
$$ \hat{y} = \hat{\theta}_0 + \hat{\theta}_1 x_1 + \hat{\theta}_2 x_2 + ... $$
특징이 1 개이고 1차항인 선형 회귀 모델
$$ \hat{y} = \hat{\theta}_0 + \hat{\theta}_1 x $$
오차 $$e = y - \hat{y}$$
손실함수 Loss function $J$
$$ J = \sum_{i=1}^n e_i $$
최소제곱법(OLS ; Ordinary Least Square)
모든 오차의 제곱합(RSS ; Residual Sum of Squares)을 최소화하는 가중치 벡터를 구하는 방법
특징이 1 개이고 1차항인 선형 회귀 모델에서
$i$번째 데이터에서의 예측값이 $ \hat{y}(x_i) = \hat{\theta}_0 + \hat{\theta}_1 x_i $
이므로, 이 때의 오차는 $e_i = y_i - \hat{y_i} = y_i - (\hat{\theta}_0 + \hat{\theta}_1 x_i) = y_i - \hat{\theta}_0 - \hat{\theta}_1 x_i $
모든 오차의 합(손실함수)이 작아야 좋은 모델이지만 부호가 서로 다른 오차를 더할 경우 상쇄되어 오차가 $-$가 나오는 등 값이 부정확해지기 때문에 모든 오차의 절대값을 취하여 더하거나 제곱하여 더한다.
$$ 손실함수J(\theta) = \sum_{i=1}^n e_i^2 = \sum_{i=1}^n ( y_i - \hat{\theta}_0 - \hat{\theta}_1 x_i )^2 $$
$\theta_0^2$와$\theta_1^2$의 계수는 모두 제곱되어 양수이므로 각각에 대한 그래프(다른 변수 상수취급)를 그리면 아래로 볼록한 그래프가 되므로, 기울기가 0일 때 오차가 최소가 된다.
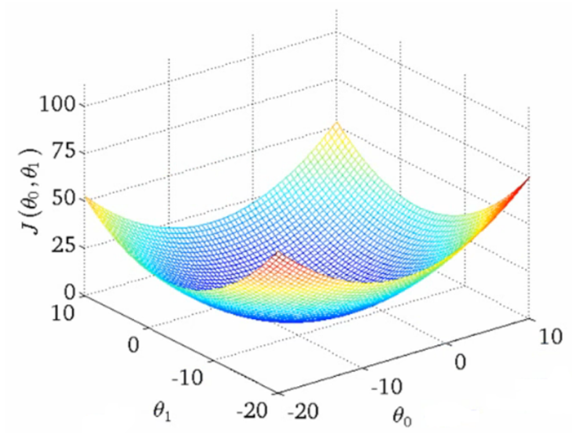
이것은 $\theta_0$와$\theta_1$에 대해서 각각 편미분한 값이 0일 때를 말하므로
$ \bar{y} = \frac{\sum_{i=1}^{n}(y_i)}{n} = y$의 평균, $ \bar{x} = \frac{\sum_{i=1}^{n}(x_i)}{n} = x$의 평균
$$ \frac{\partial f}{\partial \theta_0} = 0 \quad \blacktriangleright \quad \theta_0 = \bar{y} - \theta_1 \bar{x} $$
$$ \frac{\partial f}{\partial \theta_1} = 0 \quad \blacktriangleright \quad \theta_1 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_1 - \bar{x})^2} = \frac{S_{xy}}{S_{xx}} $$
이런 과정으로 AI모델은 실제 데이터와 예측 모델의 오차(손실함수)가 최소가 되는 모델을 만들어 예측한다.
실제로 특성이 많을 수록 예측 모델이 더 정확해지므로 모델은 매우 복잡해지고 일일이 반복을 돌리는 것보다 행렬을 만들어 프로그램을 돌리면 빠르다.

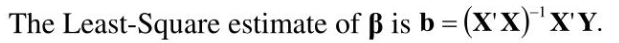
'AI > 기초' 카테고리의 다른 글
| 뉴럴 네트워크(Neural Network)의 구조 (0) | 2022.04.14 |
|---|---|
| 선형회귀모델로 보는 가중치(기울기,절편) 찾기 ; 경사하강법(GD) (0) | 2022.04.14 |
| 인공지능(AI)을 이해하기 위한 수학 기초: 미분 (0) | 2022.04.12 |
| 인공지능(AI)을 이해하기 위한 수학 기초 : 행렬, 로그, 지수, 시그마 (0) | 2022.04.12 |
| 머신러닝에 유용한 데이터셋 소스 20220509 (0) | 2022.03.14 |


댓글